Titanic

Titanic - Machine Learning from Disaster Walkthrough with Excel
kaggle
Machine Learning
Author

Ezra Safi

Published

November 23, 2025

Introduction

Today I’ll be walking through the famous Titanic - Machine Learning from Disaster competition on Kaggle.
This is my first-ever Kaggle competition, and I wanted to document everything I learned. I hope this helps anyone starting in a similar position.

If you haven’t already, check out the competition page:
👉 https://www.kaggle.com/competitions/titanic/overview

Table of Contents

  1. Downloading the Training Data
  2. Preparing the Data
  3. Setting Up the Parameters
  4. Loss Function
  5. Training a Linear Regression Model
  6. Training a Neural Network
  7. Final Thoughts

Downloading the Training Data

Download both train.csv and test.csv from the Kaggle data section:

👉 https://www.kaggle.com/competitions/titanic/data

Preparing Data

Start by loading the CSV into Excel.

Excel:
Data → Get Data → From File → From Text/CSV → select train.csv

Data Cleaning

“Garbage in, garbage out.”
Clean data is essential for model accuracy.

1. Remove Unnecessary Columns

Identifiers like PassengerId or Ticket do not help predict survival.

We will keep:

survived, pclass, age, sex, sibsp, parch, fare, embarked

Excel Action
Right-click a column → Delete → Table Columns

2. Remove Rows with Missing Values

We can see Age and Embarked contain blanks.
For simplicity, we remove rows with missing entries.

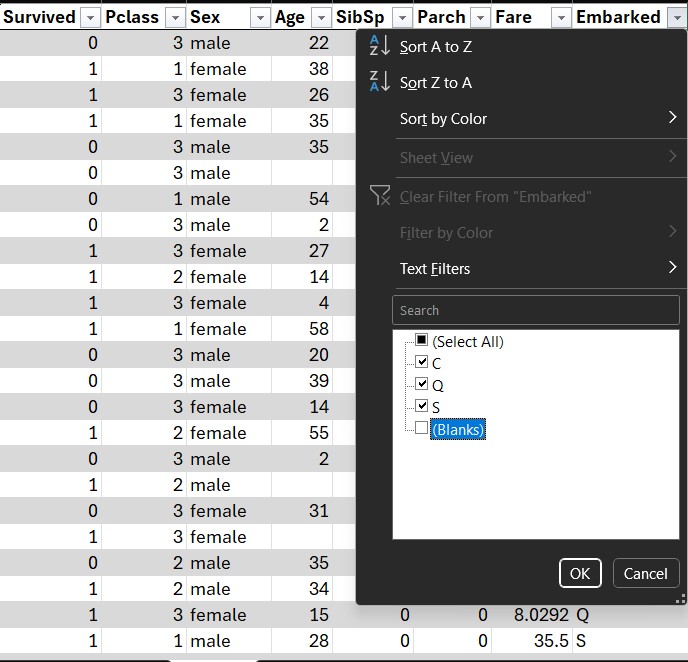
Excel Action
Filter columns → uncheck Blank

Data Scaling

Some features (like Fare) have much larger numerical ranges than others.
We scale them to prevent misleading the model.

Create new columns:

Column Formula
Age_Ratio =[@Age] / MAX([Age])
Fare_Log =LOG10([@Fare] + 1)
Ones =1

Excel Action:
Create the new scaled columns

One-Hot Encoding

Excel models cannot work with string categories.
We convert categorical data (Sex, Embarked, Pclass) into binary indicator variables.

Create the following columns:

Column Formula
Male =IF([@Sex]=“male”, 1, 0)
Pclass_1 =IF([@Pclass]=1, 1, 0)
Pclass_2 =IF([@Pclass]=2, 1, 0)
Embark_S =IF([@Embarked]=“S”,1,0)
Embark_C =IF([@Embarked]=“C”,1,0)
Ones =1

Your table should look like this:

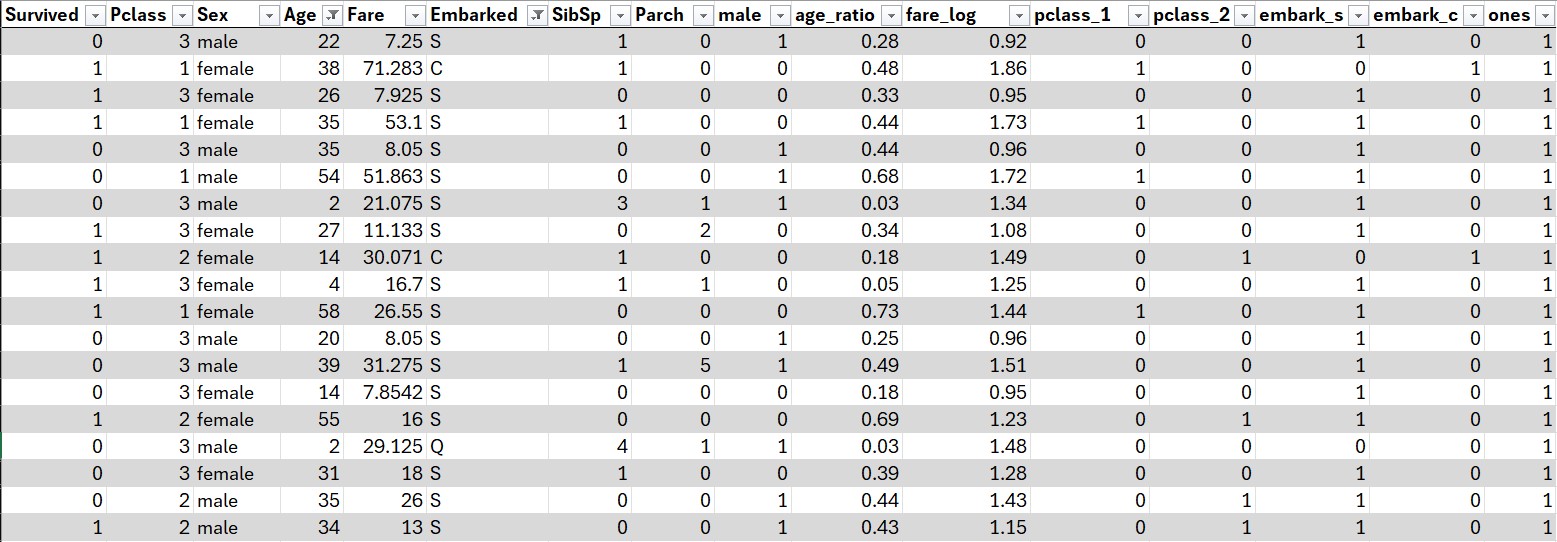
Action: Apply all the one-hot transformations

Setting Up the Parameters

Now for the fun part—creating trainable parameters.

Use: =RAND() * 2 - 1

This generates values in [-1, 1].

Action: Create the parameters table

Loss Function

We’ll use Mean Squared Error (MSE):

\text{MSE} = \frac{1}{n} \sum_{1}^{n} (y - \hat{y})^2

Where:

  • y = actual (Survived)
  • ŷ = model prediction

How Do We Compute the Prediction?

To calculate the prediction in a linear regression model, we multiply the input features by their respective weights (parameters).

Column Formula
Linear Prediction =SUMPRODUCT(data[@[SibSp]:[ones]], Params)
Loss =(data[@Survived]-[@Prediction])^2
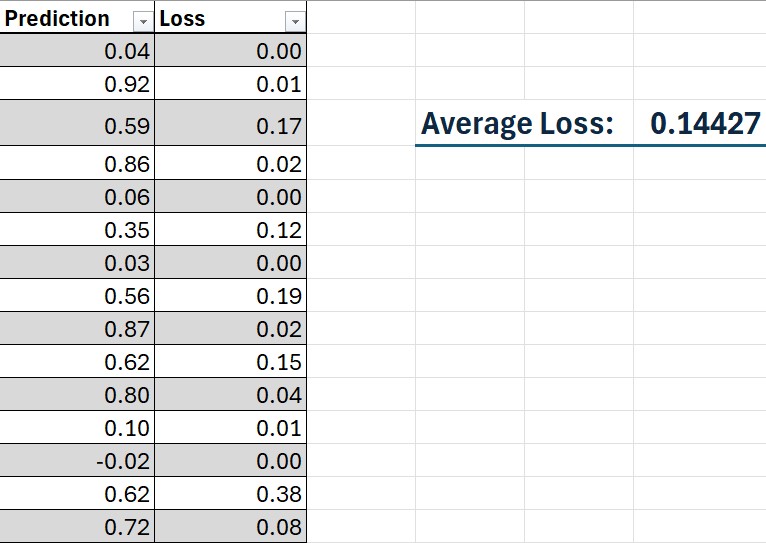
Average Loss =AVERAGE(Calculations[Loss])

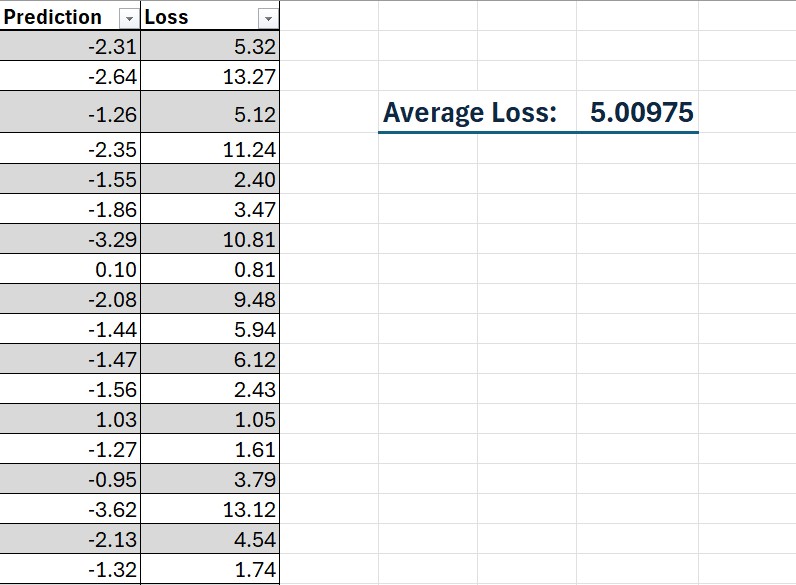
Training a Linear Regression Model

Now that we’ve set up everything, we can train the model.

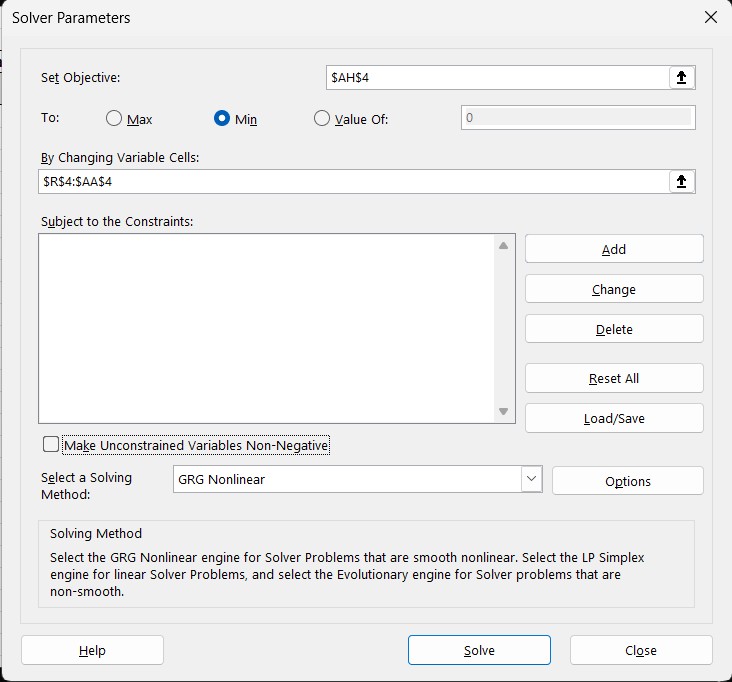
In Excel, enable the Solver add-in and configure it as follows:

  1. Set Objective → Average Loss
  2. To → Min
  3. By Changing Variables → Parameters
  4. Non-Negative → Uncheck

Click Solve and watch the Average Loss decrease. Congratulations, you’ve just trained a linear regression model in Excel!

Training a Neural Network

To improve the model, we can extend it to a Neural Network by adding an additional layer and more neurons. This is similar to our linear regression model but with added complexity.

Here’s an illustration of the model architecture:

G Neural Network Feature 2 Feature 2 Neuron 1 Neuron 1 Feature 2->Neuron 1 w Neuron 2 Neuron 2 Feature 2->Neuron 2 w Feature 1 Feature 1 Feature 1->Neuron 1 w Feature 1->Neuron 2 w Feature N Feature N Feature N->Neuron 1 w Feature N->Neuron 2 w Output Output Neuron 1->Output Neuron 2->Output
Figure 1: Neural Network Architecture

Adding a Second Neuron

After defining the network structure, we need to adjust our Excel setup to support multiple neurons, each with its own set of parameters and activation outputs.

Since our neural network contains two hidden neurons, expand the parameters table accordingly:

  • Add a second row of weights (one weight per input feature).
  • Include a second bias term.

A typical expanded parameter table looks like this:

Neuron Weight 1 Weight 2 … Weight N Bias
1 w_11 w_12 … w_1N b_1
2 w_21 w_22 … w_2N b_2

Applying the Activation Function

Each neuron’s output must be passed through a sigmoid activation function, which compresses values into the 0–1 range:

\sigma(y) = \frac{1}{1 + e^{-y}}

In Excel, implement this as: =1/(1+EXP(-[Linear Output]))

Training the Neural Network

The loss function remains the same Mean Squared Error (MSE):

L = \frac{1}{n}\sum_{i=1}^{n}(y - \hat{y})^2

To train the full neural network in Excel, configure Solver:

  • Set Objective: Average Loss
  • To: Minimize
  • By Changing Variables:
    • All weights for Neuron 1
    • All weights for Neuron 2
    • All bias terms
  • Non-Negative Constraint: Off (leave unchecked)

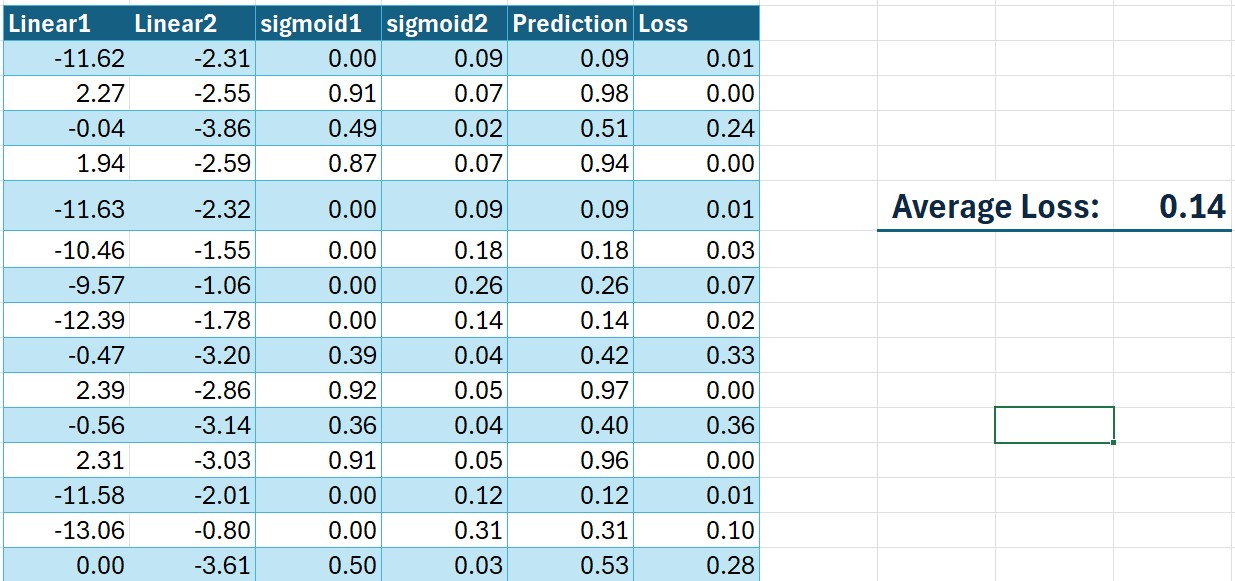
Click Solve, and Solver will iteratively optimize all parameters.

After training, your network output should resemble:

Final Thoughts

Working through this challenge brought from being completely unfamiliar with Machine Learning to being able to train a fully capable model. I’m simply mind blown that something like this can be done on Excel. I would highly recommend this kaggle challenge for anyone wanting to learn more about machine learning.

Download the Excel Workbook

Download Excel File